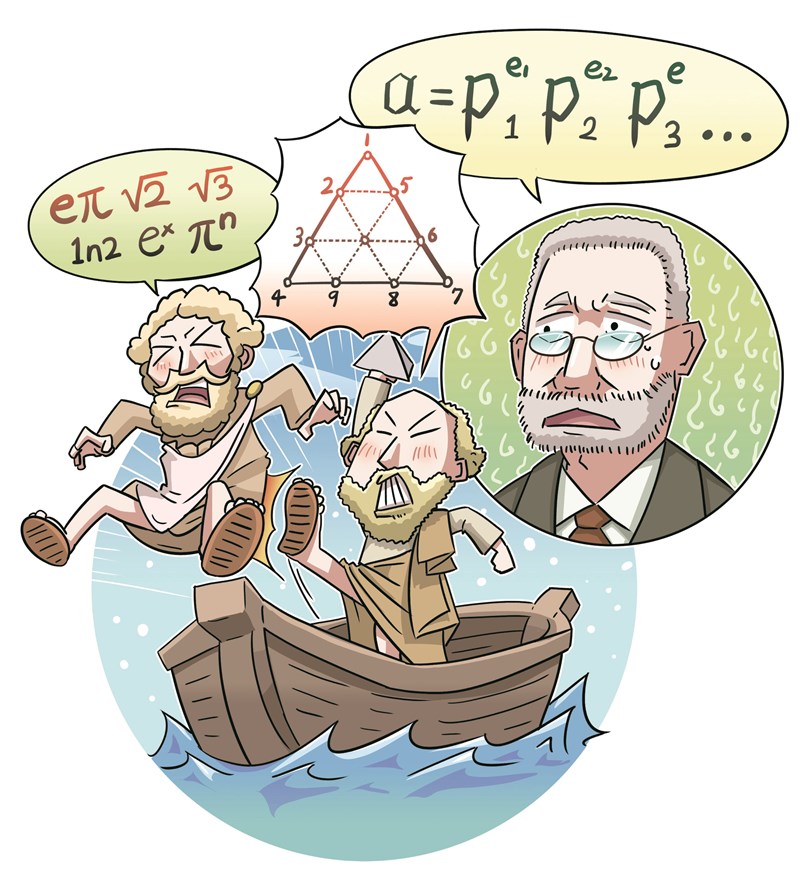文／鍾邦友

在數學裡，凡是可以被表示成為兩個整數的相除結果者，稱為「有理數」，例如整數或分數；根號2或圓周率π都是不循環的無窮小數，無法被表示成分子、分母皆為整數的分數形態，則是所謂的「無理數」。這看似簡單的數學原理，在歷史上竟然發生了一件可怕的謀殺事件！

西元前五百年左右，是數學家也是哲學家的畢達哥拉斯（Pythagoras）創立了一個帶著神祕宗教色彩的組織。這個學派的人信奉「萬物皆數」，認為宇宙間各個關係都可以用正整數與其比例，也就是使用「有理數」來表達，數字是美麗和諧、精確可控制的。

當時的人會有這種想法，是因為在任何兩個有理數之間，必定有另一個有理數存在；如1和2之間，必然其平均數3/2存在，以此類推，數字永遠無法窮盡。他們那時不知道有理數之間，還有不能被分數表達出來的「縫隙」，即無理數的存在。

兩股長1 生無理數



另外，著名的「畢氏定理」，即直角三角形斜邊長的平方，等於兩股平方和，也是畢達哥拉斯在數學史上最重要的發現之一：當兩股長為3與4，則斜邊長為5，此時三角形的三邊長自然都是整數。但是畢達哥拉斯的一位學生希帕索斯（Hippasus），發現若兩股長為1與1時，斜邊長卻是無法以分數表示的根號2，這樣一來就跟自學學派所說的「所有的數都是有理數」自相矛盾！

以現在的觀點來看，科學的真理愈辨愈明，這樣的發現當然是一件好事。可是當時的社會環境非常封閉，畢氏學派的人，生怕這件事會動搖一般人對他們的信仰與尊敬，便下令所有的人都不准走漏消息，但希帕索斯無意中對外人說出了這個驚天動地的大祕密，最後竟然被以「褻瀆神明」的罪名扔到愛琴海裡！

發現無理數的人被謀害了，但科學的真理卻不能被消滅。這個事件被稱為科學史上的第一次數學危機。直到1872年，德國的數學家戴德金（Julius Dedekind）用「有理數的分割」，建立無理數的概念，並把有理數和無理數合成了「實數」的理論，才重新為無理數建立起應有的科學地位，也成功解除這場歷經兩千多年的數學危機。