文／檸檬　

在數學中，分數是一個常見的概念，通常用來表示某個數量的一部分。不過，多數的小朋友看到「分數」兩個字就頭大，更別說解題了。今天，我們從較常見的比較分數大小入手，當我們學後，要面對分數的其他算法或應用，就會更得心應手唷！

首先，我們來談談分數是什麼？在數學中，分數是用來表示某個數量的一部分。分數通常由兩個數字組成，並且會被一橫線所隔開來，一個位於分子的位置（上方），表示數量的一部分；另一個位於分母的位置（下方），表示被分成的等分數量。例如，分數1/3表示把一個整體分成三等分中的一分。

比較分數 3種形式



接下來，我們來看看怎麼比較兩個分數的大小，比較常用的有3種方法：

1.通分比較法：這種方法通常會用於比較兩個分母不同的分數。通分比較法的步驟是將兩個分數通分為相同的分母，然後比較它們的分子大小。分子較大的分數即為較大的分數。

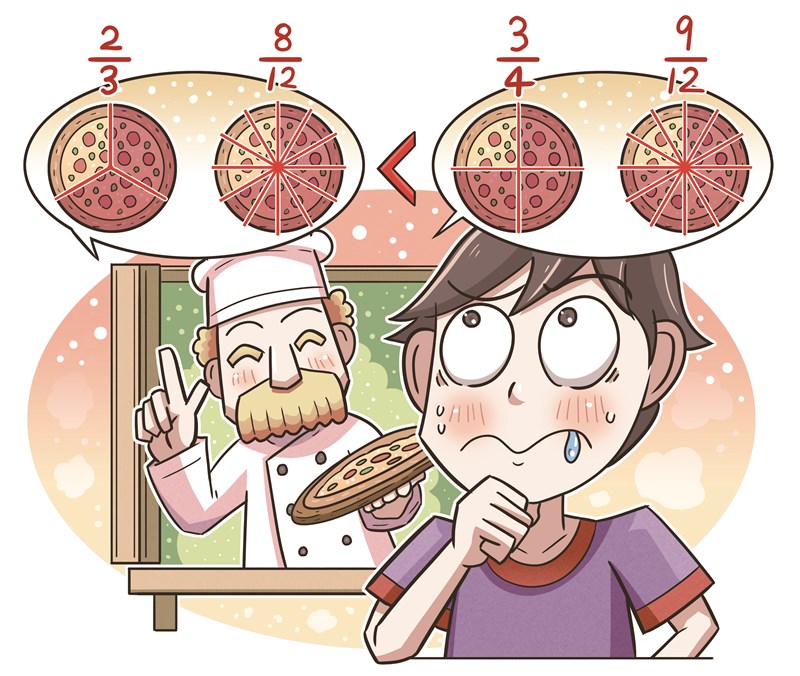
例如：比較2/3和3/4的大小。

先將這兩個分數通分為相同的分母：2/3＝8/12，3/4＝9/12

8/12＜9/12，所以2/3＜3/4

2.十進制表示法：這種方法是將分數轉換為小數表示，然後比較小數的大小。可以使用除法來將分數轉換為小數。接著比較兩個小數，數字較大的分數即為較大的分數。

例如：比較3/4和5/8的大小。

先將這兩個分數轉換為小數：3/4＝0.75，5/8＝0.625

0.75＞0.625，所以3/4＞5/8

3.轉換為百分比：這種方法是將分數轉換為百分比的形式，再比較百分比的大小。可以將分數轉換為百分比的方法是將分子除以分母，然後乘以100。比較兩個百分比時，百分比較大的分數即為較大的分數。

例如：比較7/10和11/20的大小。

先將這兩個分數轉為百分比的形式：7/10＝70%，11/20＝55%

70%＞55%，所以7/10＞11/20

生活運用 也有分數



以上是3種常用的分數比大小的方式，分數比較不僅在數學中有用，而且在日常生活中也有能派上用場。例如：當我們在商店購物時，經常會遇到折扣活動，折扣通常以分數形式表示，例如「打七折」或「買二送一」，這是兩種不同的折扣方式，該怎麼選擇呢？在廚房中烘烤小餅乾時，常常需要根據食譜去調整分量。如果食譜需要1/2杯的麵粉，而我們只有1/4杯的麵粉，我們需要判斷其他材料的分量該減少多少呢？

分數比較是數學中的一個重要概念，同時也在日常生活中具有實際應用價值。在生活中，分數比較的技巧可以應用於購物折扣、食譜調整等，對小朋友而言，掌握這些方法將有助於更容易理解分數的比較，並應用於日常生活中。通過實際應用和練習，小朋友們將能夠更自信的解決分數比較問題喔！