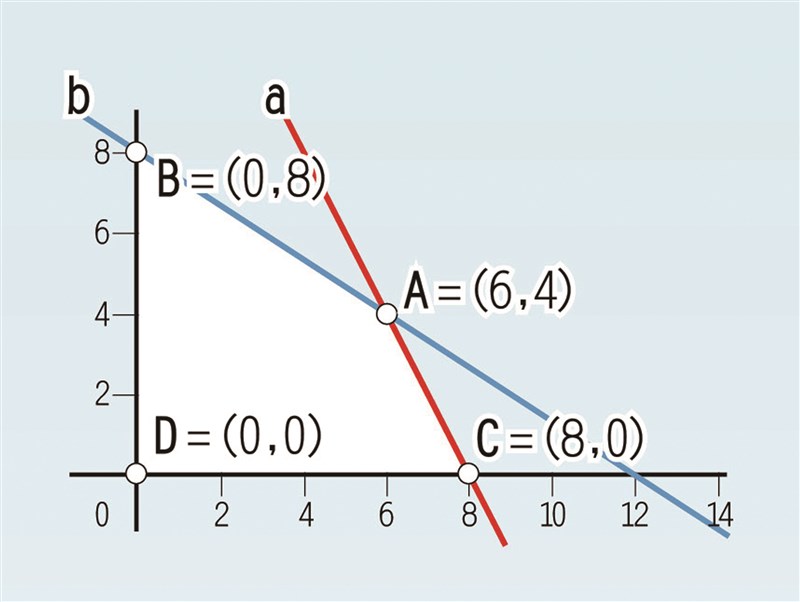
 圖中的四邊形ABCD,4個頂點,均為可能產生最佳解的極端值。我們分別將它們代入漁貨獲利的目標函數,即可發現當代入A =(6,4)時可產生極大值,也就是520萬元的最大獲利。
圖/鍾邦友
圖中的四邊形ABCD,4個頂點,均為可能產生最佳解的極端值。我們分別將它們代入漁貨獲利的目標函數,即可發現當代入A =(6,4)時可產生極大值,也就是520萬元的最大獲利。
圖/鍾邦友
文/鍾邦友
今年3月23日埃及標準時間上午7時40分時,長達400公尺的長榮海運貨櫃船「長賜輪」在航經蘇伊士運河時,受沙塵暴中的強風吹襲而偏離航道,繼而與運河底部碰撞擱淺,最後竟至完全阻塞運河。擱淺的河段又恰巧是窄小未擴建區域,其他船隻因而無法繞行,造成超過三百艘船隻排隊等候,其中至少有15艘船隻因無計可施而下錨等候。最後長賜輪於3月29日脫困,歷時約一周,造成數以百億計以上的經濟損失。
由於這條運河是亞洲和歐洲之間的快捷便道,一旦受阻,主要的替代路線是繞行非洲的好望角,航程約增加6480公里,耗時增加約9至10天的航程。倘若你是這三百艘排隊等候船隻的船東之一,日後遇到這等倒楣事,你將做何打算?在有限的航運成本及可能引發的經濟損失之下,你該選擇繼等待,抑或即刻轉向,駛向好望角?
這就是學校數學課中「線性規畫」這個單元所牽涉到的相關問題。所謂線性規畫,簡單的說,是以數學方法來研究如何在有限的人力、物力資源和市場的限制下,以最少支出得到最大收益的方法。
題目
若某船東有載運大量獅子魚的貨船數艘(獅子魚原本居住印度洋、太平洋海域,因為海水暖化,加上蘇伊士運河拓寬的關係,大量進入地中海,破壞當地生態)。倘若選擇在運河附近的港灣排隊等候,則每日平均燃料費用可降至2萬元,但漁貨就得在地中海沿岸賤價出售,獲利計40萬元,而泊港的管理費也會較高,為3萬元;如若選擇穿越直布羅陀海峽,再繞行好望角,但可沿途販售漁貨,獲利計60萬元,每日燃料費用則高達4萬元,泊港的管理費降低為2萬元。
假設原地等候與繞行好望角的航期恰巧相同,該船東又需將燃料成本控制在32萬內,泊港管理費則控制在24萬。若是期望得到最大的漁貨獲利,則船東該如何分配貨船的航行方式?
兩線交接 即最大值
我們可以先列兩個不等式:
燃料成本:4x+2y≤32
泊港管理費:2x+3y≤24
現假設該船東規畫x艘船繞行好望角,y艘船原地排隊等候:
右上圖中的四邊形ABCD,4個頂點,均為可能產生最佳解的極端值。我們分別將它們代入漁貨獲利的目標函數,即可發現當代入A =(6,4)時可產生極大值,也就是520萬元的最大獲利。
答案
船東有10艘船時,可分配6艘船繞行好望角;4艘船原地排隊等候,即可在各項成本限制之下得到最大獲利。
類似常見問題,還有工廠如何分配兩種效能不同的機器,生產某兩項產品;農人如何劃分土地,種植兩種農作物以達到最佳獲利。由於趣味多腦河版面著重在基礎學習,因此僅以兩種變數為考量,同學可自行在學校數學課,嘗試增加變數或條件之數量。
以今年初的長賜輪事件為例,尚可考量原地泊船,可放人員無薪假,以降低人事成本;或哪種方式的漁貨出售速度較快,可減少冷凍的用電成本等,都是後續供同學深入思考的方向,亦可更貼近實際的生活。