天有多高？現在的小朋友都知道天並不是像一張蓋子，根本沒辦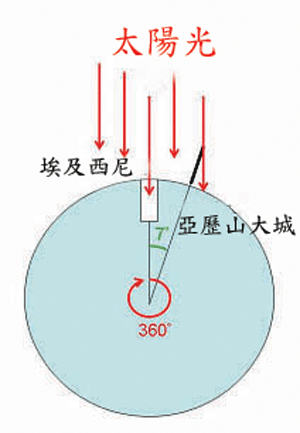法量出高度，但古人直覺地認為天是具體的，像一鍋蓋般罩著大地，《晉書‧天文志》記載：譗天圓如張蓋，地方如棋局。豃既是張蓋，就該有個高度，《周髀算經》裡寫道：譗天象蓋笠，地法復覆槃，天離地八萬里。豃這八萬里的詳細測量方式並不可得，可能和立竿測影有關。

埃及人發展幾何學

測量的問題全和數學的幾何有關，埃及人在西元前數千年發展了幾何學，這是為了尼羅河氾濫後的土地丈量所需，但古希臘人在純科學的思考下，能提出了丈量地球大小的方法，令人欽佩。西元前三世紀左右，古希臘學者厄拉托西尼（Eratosthenes）首次測量了地球的周長。厄拉托西尼有一位現今很紅的友人—阿基米德，但他本人在當時也是很出名的，受到埃及托勒密王朝的器重，被聘為亞歷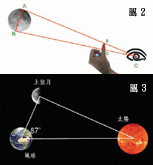山大圖書館館長，以及王子的家庭教師。厄拉托西尼發現夏至（6月22日）的時候，在埃及西尼（現埃及的阿斯旺）正午時分，太陽光可以直射到水井的底部，表示太陽是在正頭頂上，太陽光垂直照在地面，但在亞歷山大城則會有7度的傾斜（如圖一）。從幾何關係上來看，地球圓周長對應的角度是360度，而西尼到亞歷山大城的距離所對應的角度是7度，所以西尼到亞歷山大城距離的360/7倍，就是地球的圓周長。

圖一、只要知道地球是圓的，西尼到亞歷山大的圓弧長是地球圓周長的7/360。圖／曾耀寰繪製

圖二、大三角形ABC和小三角形abC互為相似三角形，邊長有一定的比例。

圖曾耀寰繪製

圖三、上弦月（或下弦月）的時候，月亮、地球和太陽形成一個直角三角形，阿力斯塔克量到的夾角是87度，實際應該是89度52分。圖／曾耀寰繪製


希臘當時用的距離單位是希臘里，厄拉托西尼得到的地球周長是25萬多希臘里，我們不是很確定詳細的換算公式，但有人認為1希臘里約0.16公里，有了圓周長，就可以算出地球的直徑，厄拉托西尼算出的地球直徑和實際的直徑只差了80多公里。從這個地球直徑便可以依序推出月亮有多大、月亮有多遠、甚至是太陽有多遠。

豎起大姆指 就可量月亮距離

在厄拉托西尼之前，一位希臘天文學家阿力斯塔克（Aristarchus）就推算出月亮的大小。上次介紹月食的時候，利用月亮經過陰影的時間推算月亮的大小是地球四分之一，就是阿力斯塔克的傑作。對阿力斯塔克而言，進一步推算月亮有多遠是很簡單的，只要豎起大拇指（如圖二），加上簡單的三角幾何，便可以推算月亮的距離。圖二是兩個相似三角形，拇指到眼睛距離和拇指大小的比例約100：1，月亮距離和月亮的直徑也是100：1，所以月亮的距離約32萬公里。

接下來阿力斯塔克可以從月亮陰晴圓缺的成因推算太陽的距離。因為月相只剩一半的上弦月或下弦月的時候，月亮和地球、太陽形成一個直角三角形（如圖三），只要測量太陽和地球連線，以及月亮和地球連線的夾角，加上月亮的距離，便可以算出太陽的距離。阿力斯塔克量到的夾角約87度，因此太陽的距離是月亮距離的20倍，不過太陽的距離應該是月亮距離的400倍，這並不表示阿力斯塔克的方法錯誤，只不過他量的夾角有誤差，實際應該是89度52分，雖然角度的誤差不大，但距離的誤差可達20倍。

這些測量的方式全賴古希臘學者對地球、月亮和太陽相對關係的正確認知，他們知道地球是圓球狀，月亮繞著地球公轉，雖然丈量的手法有些粗糙，但仍能做出令人驚訝的成就。